Using Neotoma to parse PEG in Erlang 25 February 2011
Posted by Oliver Mason in erlang, programming.4 comments
For a project I need some easy and simple way to read structured data from a text file. Initially I considered JSON, and found a JSON parser for Erlang, but then decided that this was just overkill for what I needed. Ideally there would be a better match between the data structures I needed (lists, atoms, strings) and the file format.
I then decided to use Lisp-like S-expressions; at least a simplified version thereof. The data I read from the file is basically a list which can contain other lists, strings (which technically are also just lists), and atoms. A while ago I wrote a simple Erlang module to process something similar, but that had made certain assumptions that didn’t hold anymore, and I felt something more maintainable was required. And what better way to do that than by using a formal grammar to describe the file format and a tool to generate a parser from that?
A simple and straight forward grammar formalism is PEG, Parsing Expression Grammar, and there is already an Erlang parser available for it, Neotoma by Sean Cribbs. Installation was easy, and so was writing a grammar:
list <- open elem* close;
elem <- list / atom / sstring / dstring;
atom <- [a-z0-9_]+ space*;
dstring <- '"' [^"]* '"' space*;
sstring <- "'" [^']* "'" space*;
open <- '(' space* ;
close <- ')' space* ;
space <- ' ' / '\t' / eol;
eol <- '\r\n' / '\n' / '\r';
A list is something (or nothing) enclosed in quotes (with optional spaces). An element is a choice of things, atoms are lower case letters and digits (at least one), and with strings I allow both double and single quotes. This grammar is saved in a file “terms.peg”:
Eshell V5.7.3 (abort with ^G)
1> neotoma:file("terms.peg").
ok
2> c(terms).
{ok,terms}
and you’re ready to go. I created four short one-line test files, with the following content:
- (atom)
- ( “string” )
- (foo bar)
- (())
This is the output:
3> terms:file("test1").
[["(",[]],[["atom",[]]],[")",["\n"]]]
4> terms:file("test2").
[["(",[" "]],[["\"","string","\"",[" "]]],[")",["\n"]]]
5> terms:file("test3").
[["(",[]],[["foo",[" "]],["bar",[]]],[")",["\n"]]]
6> terms:file("test4").
[["(",[]],[[["(",[]],[],[")",[]]]],[")",["\n"]]]
Not all that helpful, as there is a lot of noise in there, such as the spaces in “test2”, and all the line-breaks. So I need to go back to the AST and extract just those bits from the parse tree that I actually want. In Neotoma you can do this by adding bits of Erlang code to the grammar definition, like so:
list <- open elem* close
`[Open, Elem, Close] = Node, Elem`
;
atom <- [a-z0-9_]+ space*
`[Atom, Space] = Node, list_to_atom(Atom)`
;
dstring <- '"' [^"]* '"' space*
`[Quote, Str, Quote, Space] = Node, Str`
;
sstring <- "'" [^']* "'" space*
`[Quote, Str, Quote, Space] = Node, Str`
;
(All other lines are unchanged as in the grammar listed above)
What I do here is to split the Node into its component parts, and then discard the bits I don’t want. In the ‘list’ rule I am only interested in the elements, but not in the enclosing brackets, so I just return ‘Elem’. For the ‘atom’ I ignore the spaces and convert the matched character sequence into an atom. Now the output looks like this:
7> neotoma:file("terms.peg").
ok
8> c(terms).
{ok,terms}
9> terms:file("test1").
[atom]
10> terms:file("test2").
["string"]
11> terms:file("test3").
[foo,bar]
12> terms:file("test4").
[[]]
Much better, and just what I wanted. The ‘terms.elr’ file that neotoma generated is 7kb in size, just over 220 lines, and just under 8kb compiled.
The only issue is speed and memory consumption: on my 8GB MacBook Pro a file of less than 40k runs out of memory and crashes after 30+ seconds. If I take a part off at the end to make it 35k, the parser succeeds, but needs 35 seconds (hand-timed). So I think I will have to revisit my hand-made parser again after all… :(
UPDATE:
I had an email exchange about this with Sean, who informs me that this is a limitation of the memoisation, which creates multiple duplicates as (unoptimised) lists. So, not a fault of neotoma, but of the algorithm in general. There are ways around this, but available time to implement is as always a limiting factor!
Update/Correction to “Elegant IR with Erlang” 14 October 2010
Posted by Oliver Mason in algorithm, erlang, programming.add a comment
When I tried to actually use my implementation of tf-idf that I described in the previous post, I realised that it’s not quite what I wanted: as it is, I get a different tf-idf value for each token and each document. So with a collection of 1000 documents I get 1000 dictionaries containing the tokens in each text. However, what I really want is ONE dictionary with all the tokens in, and ONE tf-idf value for each token.
Merging the values is tricky, as it involves relative frequencies, so I needed to make some subtle changes. First, the term_freq/1 method now deals with absolute frequencies, and returns a tuple containing the frequency values and the document size in tokens, so that the relative frequencies can easily be computed if required:
term_freq(Text) ->
term_freq(Text, 0, dict:new()).
term_freq([], Sum, Dict) ->
{Dict, Sum};
term_freq([Token|Rest], Sum, Dict) ->
term_freq(Rest, Sum+1,
dict:update_counter(Token,1,Dict)).
No change really, only the terminating clause of term_freq/3 has dropped its dict:map to compute the relative values, and instead returns the tuple with the frequency dictionary and the document size.
This also requires a minor change in the inv_doc_freq/3 function, where we need to deal with the tuple and extract the dictionary from it in the second and final clause:
old
inv_doc_freq([Doc|Rest], DocNum, Dict) ->
new
inv_doc_freq([{Doc, _Sum}|Rest], DocNum, Dict) ->
The biggest change, however, is in the combined tf_idf/1 function, as the algorithm has somewhat changed. Originally the function was a full screen in the editor, but I have extracted two functions to make them easier to follow; the gain in clarity will surely outweigh the minute performance penalty…
tf_idf(Docs) ->
Idfs = inv_doc_freq(Docs),
DocLen = total_doc_size(Docs),
DocTotalFreqs = total_token_freqs(Docs),
dict:map(
fun(Key, Value) ->
dict:fetch(Key, Idfs) * Value / DocLen
end,
DocTotalFreqs).
I need to calculate the overall size (in tokens) of the full document collection, and then add up the token frequency over all documents. These have been factored out into separate functions. Then all is left is a map over all tokens to calculate the tf-idf value from the relative frequency in the document collection multiplied by the idf value as calculated earlier.
Computing the total document size is trivial: we loop over the list of term frequency dictionaries and this time extract the lengths, ignoring the actual dictionaries:
total_doc_size(Docs) ->
lists:foldl(
fun({_Doc, DocSum}, Total) -> Total + DocSum end,
0,
Docs).
And finally, that leaves computing the total frequencies of all tokens.
total_token_freqs(Docs) ->
lists:foldl(
fun({Doc, _Sum}, Current) ->
dict:fold(
fun(Key, Value, AccIn) ->
dict:update_counter(Key,Value,AccIn)
end,
Current,
Doc)
end,
dict:new(),
Docs).
Here we process the document list (as there are likely to be fewer documents than tokens) and fold each dictionary, adding the tokens with their respective frequencies to our accumulator dictionary.
Apologies for this correction; but sometimes you only really realise that a particular interpretation of an algorithm is not the right one when you actually need to use it. The curse of developing libraries without proper specification of the requirements…
Elegant IR with Erlang 11 October 2010
Posted by Oliver Mason in erlang, programming.1 comment so far
I am currently working on a project that requires processing documents. As part of that I wanted to use term weighting as used in information retrieval (IR); the individual texts I’m working with are of course of different lengths and contain different sets of words, and I didn’t want that to mess things up as it did when I initially worked with raw token frequencies only.
What I actually wanted is tf-idf, the product of term frequency (tf) and inverted document frequency (idf); essentially you see how often a word/term/token occurs in a text, and multiply that with a measure of how ‘bursty’ it is. The idea being that common words (the, of, and etc) occur in pretty much every document and are thus useless for categorisation of the content. In a way it is a more sophisticated approach to using a stop word list. Sophisticated because you don’t have to create such a list, and it is also not binary include/exclude, but assigns each token a continuous weight depending on its distribution.
Term Frequency
This is simply the relative frequency of occurrence, the number of times a token occurs in the text divided by the text length. As input I assume that the text has already been tokenised and is represented as a list of tokens. The output should be a dictionary (ie a set of key/value tuples) with each token as a key and its tf as the value:
term_freq(Text) ->
term_freq(Text, 0, dict:new()).
term_freq([], Sum, Dict) ->
dict:map(
fun(_Key, Value) -> Value / Sum end,
Dict);
term_freq([Token|Rest], Sum, Dict) ->
term_freq(Rest, Sum+1,
dict:update_counter(Token,1,Dict)).
In case another token is available, I simply update its frequency by one, add one to the text size, and re-run the function on the rest of the text. If no more tokens are left, then I map the dictionary (which at this point contains absolute frequencies) to another dictionary by way of dividing each value by the text size; this new dictionary is then returned.
Inverted Document Frequency
For the idf I count how many documents each token occurs in, and divide the total number of documents by that number; so the rarer the token, the larger the resulting value. The token the should just give a result of 1.0; however, to make it a bit more complicated we then take the logarithm (base-10) of it, so that the final value will be greater than or equal to zero.
This time the input is a list of dictionaries, one for each document. The dictionary representing each document is the output of our term_freq/1 function, ie the keys are the tokens, and the values the term frequencies. We don’t really care about the frequencies here, as they all will be greater than zero – a word that does not occur in a text will not be a key in the respective dictionary. As output we will have a single dictionary of all tokens that occur in our document collection, with the values being the idf of each token.
inv_doc_freq(Docs) ->
inv_doc_freq(Docs, 0, dict:new()).
inv_doc_freq([], DocNum, Dict) ->
dict:map(
fun(_Key, Value) -> math:log10(DocNum/Value) end,
Dict);
inv_doc_freq([Doc|Rest], DocNum, Dict) ->
inv_doc_freq(Rest, DocNum+1,
dict:fold(
fun(Key, _Value, AccIn) ->
dict:update_counter(Key,1,AccIn) end,
Dict,
Doc)
).
Again we iterate over all elements of our input list (ie the documents), and this time we iterate over all tokens of the document using a dict:fold/3 function, by adding 1 to the count for each token of the current document that we have already encountered, or entering it with a frequency of 1 if we haven’t yet. We also increment the document count by 1. This time the dict:map/2 function performs the calculation for the idf value as soon as we have reached the end of our document list.
tf-idf
At this stage we have a dictionary for each document containing the term frequencies, and a dictionary for the whole document collection containing the inverted document frequencies for all the tokens. Combining the two we then get the value for the tf-idf, which is different for each document (so the output is a list of dictionaries, one per document).
To make things easier, the call to compute the idf is integrated into the tf_idf/1 function, so the input is the same as for the inv_doc_freq/1 function, a list of term frequency dictionaries:
tf_idf(Docs) ->
Idfs = inv_doc_freq(Docs),
lists:map(
fun(TFs) -> dict:map(
fun(Key,Value) -> Value *
dict:fetch(Key, Idfs) end,
TFs) end,
Docs).
Here we map the list of term frequency dictionaries (Docs) to a list of dictionaries containing the tf-idf values. For this mapping we map each (document) term frequency dictionary to the respective (document) tf-idf dictionary by multiplying each token’s term frequency by its idf value as computed by inv_doc_freq/1.
Summary
Calculating a set of values from texts is very concise with Erlang. In languages like C or Java one would have to code various (nested) loops, but this can easily be accomplished by using the map and fold functions that operate on lists and dictionaries in Erlang. It does need a bit of mental acrobatics, but if you are familiar with Prolog, then the basic structure of an Erlang program is not too difficult to follow. It’s those nested mappings that sometimes can be a little confusing.
The beauty of Erlang, of course, is that each map can be done in parallel; if you have a large list of documents and a processor with several cores then it is not hard to make use of its full power by simply using a parallel map function. To do this in other languages where nested loops are used in place of the map function is not trivial.
So Erlang is not only very concise, but it can also be future-proof by allowing easy concurrency.
Go – Went – Gone 30 December 2009
Posted by Oliver Mason in erlang, programming.add a comment
I did play around with the unhelpfully named ‘go’ programming language, another output of the don’t-be-evil company. Trying to find any web resources for it is pretty much impossible, for one thing because it was too new, and then because of the name. I would have expected something more search-friendly from the number 1 web search engine!
There were a few things I liked about go. It’s smallish, C-like, has garbage collection, built-in support for concurrency, and unicode strings. Hash-tables (‘maps’) as a first-class data type. A nicely-looking set of libraries for all sorts of purposes. Not quite fast, but with lots of scope for performance improvements. No header files. First class support for unit tests.
This was looking attractive as opposed to Erlang, which is older and more mature/stable, but still not very high-performance, has slightly awkward string handling, and exactly three data types (list, tuple, atom). And a Prolog-style syntax with a number of inconveniences about the use of commas, semicolons, and full stops. Editing a clause is never straightforward.
I have since abandoned go again. It also has inconsistencies (the use of ‘new’ for some data types and ‘make’ for others), and worst of all, there was so much talk about wanting to add generics to the language that I fear they will become a feature of it. I don’t like generics: they seem to me to be more trouble than it’s worth. They make code really hard to read, and inflexible. They might make some kinds of bugs impossible, but in my view that is a feeble gain for wrecking a language. As Knuth (I think) said, part of writing programs is aesthetics. I cannot like Java code full of abstract type annotations. Objective-C is so much cleaner in comparison. And so was go, until now.
Another reason is the concurrency support. Go uses pipes for that, which seems awkward. I much prefer Erlang’s mailboxes, which neatly work together with pattern matching to respond to certain messages and ignore others. You do not need to worry about the order in which messages arrive as much, and the whole communication process is a lot easier with only the basic data types.
So I’m going back to Erlang. I will dig out the string library that I started, and get back into thinking recursively. At least I know where I am with it, and it is not suddenly going to change!
Building the database without glare 5 May 2009
Posted by Oliver Mason in Apple, erlang, iphone, objective-c, programming.1 comment so far
DAY 7 sounds like a lot, but again I’m only working a few hours in the evening after the kids have gone to bed. I have the feeling that there is a lot of ‘boilerplate’ code to write in Objective-C, or Cocoa at least. But then, that might be the problem with GUI-related programming. Erlang doesn’t nearly need as many lines to accomplish something, anything really! But then, the kind of Erlang programs I’ve been working on are basic R&D text-only affairs, not MVC-style user interface programming.
I have today learned how to turn off the iPhone program icon glare (add UIPrerenderIcon=true to info.plist in the bundle), which I think looks better on my icon which had a horizontal line just about where the glare-line was. I also created a SQLite database from a text file. Next I will need to integrate the DB with the table view, for the first part of actual functionality. I keep switching between chapters in the textbook, the one which builds tables and the one which deals with persistent storage. Why did nobody think of doing a database-backed table view? Need to check Apple’s sample code, they’ve got a book-storage one which might do that.
The depressing bit is that I write a little Noddy-program, and it takes me ages. Mainly getting used to Cocoa, Xcode, and Objective-C, but also going back to no garbage collection, and shifting data between classes I know not well at all (NSString, NSArray, etc). I think my niche will be little utilities, rather than glorious games!
Thinking Erlang, or Creating a Random Matrix without Loops 26 February 2009
Posted by Oliver Mason in erlang, misc, programming.11 comments
For a project, my Erlang implementation of a fast PFNET algorithm, I needed to find a way to create a random matrix of integers (for path weights), with the diagonal being filled with zeroes. I was wondering how best to do that, and started off with two loops, an inner one for each row, and an outer one for the full set of rows. Then the problem was how to tell the inner loop at what position the ‘0’ should be inserted. I was thinking about passing a row-ID, when it suddenly clicked: lists:seq/2 was what I needed! This method, which I previously thought was pretty useless, creates a list with a sequence of numbers (the range is specified in the two parameters). For example,
1> lists:seq(1,4). [1,2,3,4] 2> lists:seq(634,637). [634,635,636,637] 3> lists:seq(1000,1003). [1000,1001,1002,1003]
Now I would simply generate a list with a number for each row, and then send the inner loop off to do its thing, filling the slot given by the sequence number with a zero, and others with a random value.
But now it gets even better. Using a separate (tail-)recursive function for the inner loop didn’t quite seem right, so I thought a bit more about it and came to the conclusion that this is simply a mapping; mapping an integer to a list (a vector of numbers, one of which (given by the integer) is a zero). So instead of using a function for filling the row, I call lists:seq again and then map the whole thing. This is the final version I arrived at, and I’m sure it can still be improved upon using list comprehensions:
random_matrix(Size, MaxVal) ->
random:seed(),
lists:map(
fun(X) ->
lists:map(
fun(Y) ->
case Y of
X -> 0;
_ -> random:uniform(MaxVal)
end
end,
lists:seq(1,Size))
end,
lists:seq(1,Size)).
This solution seems to be far more idiomatic, and I am beginning to think that I finally no longer think in an imperative way of loops, but more in the Erlang-way of list operations. Initially this is hard to achieve, but with any luck it will become a lot easier once one is used to it. Elegance, here I come!
Example run:
4> random_matrix(6,7). [[0,1,4,6,7,4], [3,0,5,7,5,4], [5,1,0,2,5,2], [4,2,4,0,3,1], [4,4,3,3,0,1], [5,7,3,2,2,0]]
Note: I have used random:seed/0 above, as I am happy for the function to return identical matrices on subsequent runs with the same parameters. To get truly random results, that would have to be left out. However, for my benchmarking purposes it saved me having to save the matrix to a file and read it in, as I can easily generate a new copy of the same matrix I used before.
Fast PFNETs in Erlang 14 February 2009
Posted by Oliver Mason in algorithm, erlang, programming.2 comments
Introduction
Pathfinder Networks (PFNETs) are networks derived from a graph representing proximity data. Basically, each node is connected to (almost) every other node by a weighted link, and that makes it hard to see what’s going on. The Pathfinder algorithm prunes the graph by removing links which are weighted higher than another path between the same nodes.
For example: A links to B with weight 5. A also links to C with weight 2, and C links to B with weight 2. Adding up the weights, A to B direct is 5, A to C to B is 4. Result: we remove the link from A to B, as the route via C is shorter. There are different ways to calculate the path lengths (using the Minkowski r-metric), but you get the general idea. The resulting PFNET has fewer links and is easier to analyse.
In Schvaneveldt (1990) an algorithm for computing PFNETs is given, but it is rather complex and computationally intensive. There is an improved algorithm called Binary Pathfinder, but that is apparently more memory intensive. Not very promising so far, but then along comes A new variant of the Pathfinder algorithm to generate large visual science maps in cubic time, by Quirin, Cordón, Santamaría, Vargas-Quesada, and Moya-Anegón. This algorithm is a lot faster (by about 450 times), but has one disadvantage: speed is traded in for flexibility. The original Pathfinder algorithm has two parameters, r (the value of the Minkowski metric to be used) and q (the maximum length of paths to be considered). The fast algorithm only has r, and always uses the maximum value for q (which is n-1). I know too little about the application of PFNETs to say whether this is important at all; for the uses I can envisage it does not seem to matter.
As added bonus, the algorithm in pseudo code in Quirin et al. is very short and straightforward. They’re using a different shortest-path algorithm to identify, erm, shorter paths. And then it’s very simple to prune the original network.
A picture tells more than 1K words, so here instead of 2000 words the before and after, graph layout courtesy of the graphviz program:

Fig 1: A network example (from Schvaneveldt 1990)
Here, each node is linked to every other node. Running the PFNET algorith on it, we get the output shown in the second figure.
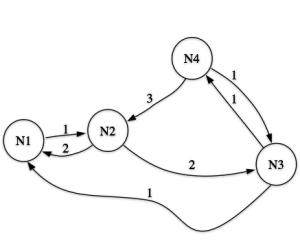
Fig 2: A PFNET generated from the previous graph
If you compare the output with the actual result from Schvaneveldt’s book (p.6/7), you’ll realise that it is not identical, and the reason for that is that the example there limits the path-length, using the parameters (r = 1, q = 2) rather than (r = 1, q = n-1) as in the example shown here. As a consequence, the link from N1 to N4 (with a weight of 5) disappears, because of the shorter path (N1-N2-N3-N4, weight 4). But that path is too long if q is just 2, and so it is kept in Schvaneveldt’s example.
Implementation
It is not possible to implement the pseudo-code given in Quirin et al directly, as they use destructive updates of the link matrix, which we obviously cannot do in Erlang. But the first, naïve implementation, is still quite short. The input graph is represented as a matrix (n x n) where each value stands for the link weight, with zero being used to indicate non-existing links. I have written a function that creates a dot file from a matrix, which is then fed into graphviz for generating images as the ones shown above.
There are basically two steps: creating a matrix of shortest paths from the input matrix, and then generating the PFNET by comparing the two matrices; if a certain cell has the same value in both matrices, then it is a shortest path and is kept, otherwise there is a shorter path and it’s pruned. Here is the main function:
find_path(Matrix) ->
Shortest = loop1(1,length(Matrix),Matrix),
generate_pfnet(Matrix, Shortest, []).
Next we have the three loops (hence ‘cubic time’!) of the Floyd-Warshall shortest path algorithm to create the shortest path matrix:
loop1(K,N,Matrix) when K > N ->
Matrix;
loop1(K,N,Matrix) ->
NewMatrix = loop2(K,1,Matrix,
Matrix,[]),
loop1(K+1,N,NewMatrix).
loop2(_,_,_,[],Acc) ->
lists:reverse(Acc);
loop2(K,I,D,[Row|Rest],Acc) ->
NewRow = loop3(K,I,1,D, Row, []),
loop2(K,I+1,D,Rest,[NewRow|Acc]).
loop3(_,_,_,_, [], Acc) ->
lists:reverse(Acc);
loop3(K,I,J,D, [X|Rest], Acc) ->
loop3(K,I,J+1,D, Rest,
[min(X, get(I,K,D) + get(K,J,D))|Acc]).
The final line implements the Minkowski metric with r = 1; this could be expanded to include other values as well, eg r = 2 for Euclidean, or r = ∞ (which seem to be the most common values in use; the latter means using the maximum weight of any path component along the full path).
And here are two utility methods, one to find the smaller of two values, and one to retrieve an element from a matrix (which is a list of rows). There is something of a hack to deal with the fact that zero does not mean a very small weight, but refers to a non-existing link:
min(X, Y) when X < Y -> X;
min(_X, Y) -> Y.
get(Row, Col, Matrix) ->
case lists:nth(Col,
lists:nth(Row, Matrix)) of
0 -> 999999999;
X -> X
end.
And finally, generating the PFNET by comparing the two matrices (again, awful hack included):
generate_pfnet([],[],Result) ->
lists:reverse(Result);
generate_pfnet([R1|Rest1], [R2|Rest2], Acc) ->
Row = generate_pfrow(R1,R2,[]),
generate_pfnet(Rest1, Rest2, [Row|Acc]).
generate_pfrow([],[],Result) ->
lists:reverse(Result);
generate_pfrow([C|Rest1], [C|Rest2], Acc) ->
case C of
999999999 -> C1 = 0;
_ -> C1 = C
end,
generate_pfrow(Rest1, Rest2, [C1|Acc]);
generate_pfrow([C1|Rest1], [C2|Rest2], Acc) ->
generate_pfrow(Rest1, Rest2, [0|Acc]).
Discussion
So this is the basic code. It works, but there is scope for improvement.
- it only currently generates PFNETs with (r = 1, q = n-1)
- there is no parallelism, hence it’s not really making use of Erlang’s strengths.
- the three loops don’t look very elegant, and could probably be replaced by list comprehensions
Because of the matrix being updated, it doesn’t look that easy to parallelise the processing, but it would work at the level of updating the individual rows. If that can be done in parallel, it would probably provide some speed-up (provided the matrix is not of a trivial size). So the first step would be to change the matrix processing using lists:map/2, and replacing this then by pmap, as described in this article by Dave Thomas.
Once the code is up to scratch with full parallelism, and tested on larger matrices I will probably put it up on Google Code in case other people are interested in using it. If you have any suggestions, tell me in the comments!
References
- Schvaneveldt, R. W. (Ed.) (1990) Pathfinder Associative Networks: Studies in Knowledge Organization. Norwood, NJ: Ablex. The book is out of print. A copy can be downloaded from the Wikipedia page at http://en.wikipedia.org/wiki/Pathfinder_Networks
- Quirin, A; Cordón, O; Santamaría, J; Vargas-Quesada, B; Moya-Anegón, F (2008) “A new variant of the Pathfinder algorithm to generate large visual science maps in cubic time”, Information Processing and Management, 44, p.1611-1623.
Erlang String Issue 9 September 2008
Posted by Oliver Mason in erlang, programming.5 comments
I could never really understand people complaining about Erlang’s lack of a string data structure; having them represented as lists seemed fine, especially as there is no problem with representing unicode characters that go beyond 255. The increased size didn’t bother me: people worried about that when unicode first arrived and it didn’t really turn out as a big issue. And I do a lot of processing of large texts.
However, working on a basic YAML library for Erlang (see code repository) I ran into a problem where I least exected to be one: generating a YAML representation of a data structure.
Parsing basic YAML (just lists and mappings) was a piece of cake in the end (ignoring the more, erm, arcane bits of the YAML spec), and writing it seemed to be trivial. However, when it comes to writing out a list the problems start. I cannot differenciate between a list of numbers and a string. Hence, I cannot decide which way to represent it in YAML, as a string or a list of numbers.
This is only a human-factor issue: writing it as a list of numbers and then reading it in again obviously gives identical results, so for serialisation purposes it’s fine. But when editing the file I don’t really fancy looking up the ASCII codes for all the letters I want to change. A purely ‘presentational’ issue, but a tricky one.
Solutions? I could check any list if all the elements are in the range of readable characters, which I assume is what the Erlang VM does when printing something. But that’s a hack, really. Another solution is to go the whole hog and introduce a string type, presumably something like ‘{string, [45,64,…]}’. Then I can easily make the decision how to write it out. And parsing would be easy as well.
Now, that looks like a good idea, but it would interfere with the way most other programs use strings. And the string library wouldn’t work. So I guess I have to write my own.
My current plan is to allow various representations of strings, so that the data structure will actually be ‘{string, TYPE, DATA}’, where TYPE could be ‘list’ (the current way), ‘binary’ (a binary in UTF-8 format), ‘rope’ (a different approach to strings, see description with Java code). Other representations could be added at a later stage. There would be a function estring:to_list(string), which would convert the string into a list for use with the string library, and estring:to_string(list) would create a string from the given list. The default representation would probably be a binary, as that can in turn be used as a component of a rope easily once something gets added to it.
Another alternative would be to use Starling, but I’m not too keen on it as it’s not pure Erlang, using a C/C++ library under the hood.
How do you deal with strings?
UPDATE: Here’s a discussion about the same problem in the context of JSON: http://www.lshift.net/blog/2007/09/13/how-should-json-strings-be-represented-in-erlang
Replacing a stack with concurrency 23 April 2008
Posted by Oliver Mason in erlang, NLP, programming.4 comments
For some language processing task I needed a reasonably powerful parser (a program to identify the syntactic structure of a sentence). So I dug out my copy of Winograd (1983) (“Language as a Cognitive Process”) and set about implementing an Augmented Transition Network parser in Erlang.
Now, the first thing you learn about natural language is that it is full of ambiguities, and so there will always be several alternatives available, several possible paths through the network which defines the grammar. The traditional solution is to dump all the alternatives on a stack, and look at them when the current path has been finished with. You can either go depth-first, where you complete the current path before you get the next one off the stack, or breadth-first, where you advance all paths by one step at a time, kind of pseudo-parallel.
Having to deal with a stack is tedious, as you need to keep track of the current configuration: which network are you at, what node, what position in the sentence, etc. But then, it occurred to me, there’s an easier way to do it (at least it’s easier in Erlang!): every time you come to a point where you have multiple alternatives, you spawn a new process and pursue all of them in parallel.
The only overhead you need is a loop which keeps track of all the processes currently running. This loop receives the results of successful paths, and gets notified of unsuccessful ones (where the process terminates without having found a valid structure). No need for a stack, and hopefully very efficient processing on multi-core machines as a free side-effect.
I’m still amazed how easy it was to implement. I wouldn’t have fancied doing that in Java or even C. For my test sentences I had about 8 to 10 processes running in parallel most of the time, but it depends on the size of the grammar and the length of the sentence really. What I liked about this was that it seemed the natural way to do in Erlang, where working with processes is just so easy.
And also, another nail in the coffin for the claim that you can’t use Erlang for handling texts easily!